2. Математические основы хеджирования

2.1. Оценка степени взаимозависимости переменных

Для того чтобы успешно осуществлять хеджирование, необходимо чётко знать, как зависят друг от друга имеющаяся открытая позиция банка и потенциальный инструмент, которым данная позиция будет хеджироваться. Одним из самых простых показателей степени зависимости двух показателей между собой является ковариация. Формула для вычисления ковариации выглядит следующим образом [11, стр. 222]:

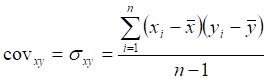,                                                                              (2.1)

где x_i и y_i - , показатели, а  и - средние значения показателей.

            Ковариационный анализ посвящён определению степени взаимо­связи двух рядов величин, которыми, в зависимости от рассматрива­емых инструментов, могут быть процентные ставки, обменные курсы и т. п. Если два ряда данных возрастают и убывают одновременно, то их ковариация является положительной. Если, однако, ряды являют­ся независимыми, то имеет место нулевая ковариация. При противо­положном изменении обоих рядов ковариация является отрицатель­ной.

Ковариации нескольких переменных удобно отражать в виде дисперсионно-ковариационной матрицы.

            В таблице 1 показаны ковариации всех возможных пар из группы трех активов. Ковариация переменной с ней самой равняется дисперсии этой переменной.

 

Таблица 1. Дисперсионно-ковариационная матрица трех активов

	X	Y	Z
X	xx	xy	Xz
Y	yx	yy	Yz
Z	zx	zy	Zz

 

  Коэффициент корреляции удобнее использовать, чем ковариацию, так как в нем преодолевается зависимость от числа наблюдений, кроме того, он независим от единиц измерения исследуемых величин.

Для исследований в основном используется линейный коэффициент корреляции, обычно называемый Пирсоновским коэффициентом корреляции, хорошо применимый для линейных связей.

Линейный коэффициент корреляции между двумя рядами Х и Y определяет­ся по следующей формуле [11, стр. 224]:

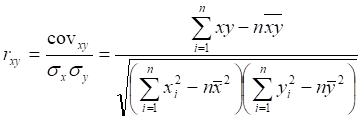 ,                                                            (2.2)

где σ_x и σ_y – среднеквадратичное (стандартное) отклонение значений рядов X и Y соответственно.

Коэффициенты корреляции также могут быть представлены в виде матриц. В таблице 2 показаны коэффициенты корреляции всех возможных пар из группы трех активов.

 

Таблица 2. Дисперсионно-корреляционная матрица трех активов

	X	Y	Z
X	1	xy	xz
Y	yx	1	yz
Z	zx	zy	1

 

Устойчивость корреляционной зависимости между двумя рядами процентных ставок или цен может предоставить очень важную ин­формацию для определения того, может ли один инструмент быть использован для хеджирования другого.

Корреляционный анализ очень прост при наличии опубликован­ных и доступных данных по ценам. Но при его подсчёте исходят из того, что переменные, для которых он рассчитывается, измерены точно и однозначно. Однако на практике работы финансовых рынков это далеко не всегда так. Это связано не только со сложностью правильного выбора самих переменных, но и с тем, что не все данные попадают в исследуемую выборку, а некоторые данные являются «неверными» котировками, ошибочно выставляемыми дилерами в информационные системы[3]. Таким образом, причинами несоответствия могут быть как случайные, так и сознательные факторы.

Частично решает эту проблему применение коэффициента ранговой корреляции[4]. Формула для его расчёта выглядит следующим образом:

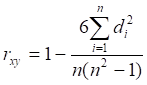,                                                                                                      (2.3)

где d_i - разница между парами рангов[5].

Нельзя однозначно утверждать, какой именно коэффициент корреляции даст более точный результат, но, когда речь идёт о долгосрочных данных, более точным будет линейный коэффициент корреляции.

Коэффициент детерминации обычно применяется для расчёта тесноты нелинейной связи. Данный коэффициент вычисляется путём возведения в квадрат коэффициента корреляции [11, стр. 228]:

.                                                                                             (2.4)

Из этой формулы видно, что данный коэффициент не даёт возможность выявлять направление связи. Тем не менее, он помогает определять зависимость одной переменной от изменения другой и именно в этом его главное предназначение. Коэффициент детерминации обычно выражается в процентах от 0% до 100%. Если коэффициент равен 0%, то это означает полное отсутствие связи между переменными. Если же коэффициент достигает 100%, то существует самая тесная связь.

Важно определиться с тем, какой факт является определяющим. Переменные могут быть ведущими, ведомыми или зависимыми и независимыми соответственно. В этой связи изменение ведущего показателя приводит к изменению ведомого, но никак не наоборот.

Переменные x и у между собой равны, и заранее отвести роль какой-либо из них ведущей или ведомой нельзя. Это требует от исследователя составления логической модели взаимозависимости переменных.

Иногда также рассчитывают коэффициент недетерминации, который равен 1 минус коэффициент детерминации. Коэффициент недетерминации показывает, в какой степени изменение одной переменной не зависит от изменения другой переменной.

«Бета»-коэффициент является частным случаем анализа взаимосвязей между двумя переменными.  Данный коэффициент оценивает меру чувствительности одной переменной (обычно доходности конкретного инструмента) к другой переменной (среднерыночной доходности или доходности портфеля).

«Бета»-коэффициент рассчитывается как отношение ковариации двух переменных к дисперсии второй переменной [11, стр. 229]:

,                                                                                                                (2.5)

где σ_xy - ковариация переменных х и y, σ²_x - дисперсия переменной x.

Если «бета»-коэффициент больше единицы, то это означает, что изменчивость доходности конкретного инструмента выше, чем доходности инвестиций в рыночный портфель или один из фондовых индексов. Если таким инструментом является акция, то её называют агрессивной.

Если «бета»-коэффициент меньше единицы, то это означает, что изменчивость доходности конкретного инструмента ниже, чем доходности инвестиций в рыночный портфель или один из фондовых индексов. Такую акцию называют оборонительной.

Если же «бета»-коэффициент равен единице, то изменчивость доходности конкретного инструмента будет точно соответствовать изменчивости среднерыночной доходности рыночного портфеля или фондового индекса.

2.2.       Регрессионный анализ

 

Коэффициент корреляции может показать, насколько сильна связь между переменными. Для того чтобы объяснить эту связь необходимо разработать теорию причинно-следственной связи, построить модель, которая отражает гипотетическую связь, и затем протестировать модель статистически. Для этого используется регрессионный анализ. С помощью регрессионного анализа строится и проверяется модель связи одной зависимой (эндогенной) и одной и более независимыми (экзогенными) переменными (их также называют регрессорами). Различают кросс-секционную регрессию (связь между переменными в определенный момент времени) и регрессию временных рядов (в течение следующих друг за другом временных периодов).

Рассмотрим регрессионный анализ для простой линейной зависимости между зависимой переменной Y и одной независимой X  [15, стр. 262]:

Y = a + βХ+e,                                                                                                                   (2.6)

где α – постоянная, отражающая значение Y при X=0, β – коэффициент регрессии («бета»-коэффициент), e – ошибка или значение помехи (оценивает влияние других факторов, не включённых в модель).

Для статистической проверки взаимосвязи чаще других используется метод наименьших квадратов. Он даёт наилучшие линейные несмещённые оценки.

Допущения при расчёте:

-        линейная зависимость между переменными;

-        значение ошибки e_i нормально распределено со средней, равной нулю, и постоянной дисперсией σ²;

-        значения e независимы друг от друга, т.е. факторы, которые послужили причиной ошибки для одной из величин Y, не приводят автоматически к ошибкам для всех наблюдений Y (т.е. данные неавтокоррелированы).

Коэффициенты можно найти по следующим формулам [15, стр. 270]:

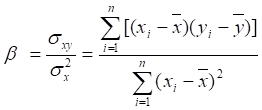,                                                                         (2.7)

.                                                                                                      (2.8)

        Значение фактической ошибки e вычисляется как фактическая разница между фактическими значениями переменной y_i и рассчитанными значениями исходя из формулы линейной регрессии [11, стр. 233]:                                                                

.                                                                                                          (2.9)

 

        Можно использовать как метод простой линейной, так и множест­венной регрессии. Множественную регрессию следует использовать для анализа зависимости между более чем двумя переменными. На­пример, зависимость между ценой облигации спот и ценой фьючер­сного контракта на облигацию и возможное внешнее влияние на эти инструменты, допустим, обменного курса. В этом случае линейная регрессионная зависимость между ценой облигации и ценой фьючерс­ного контракта имела бы следующую форму [7, стр. 13]:

Цена облигации Х =а+b* (Цена фьючерсного контракта) +

+с*(Курс конвертации Y) ...                                                                                       (2.10)

При использовании регрессионных методов для определения коэффициентов хеджирования возникают следующие проблемы:

-        «исторические» зависимости между двумя взаимосвязанными рядами процентных ставок могут быть нестабильными, и имеющиеся критерии изменчивости цен могут быть непригодными для прогнозирования относительной изменчивости цен в будущем;

-        использование слишком короткого периода для исследования зависимости между инструментами может быть недостаточным для получения результата, отражающего истинное положение дел (для инструментов с длительными сроками погашения могут отсутствовать длинные ряды данных, если операции с этими инструментами производились в течение лишь короткого периода времени).

2.3. Критерии оценки процентного риска

Можно выделить три критерия процентного риска: эластичность процентной ставки, систематический коэффициент процентной ставки и дюрацию. Дюрация является показателем ценовой чувствительности и изменчивости. Это синтетический показатель оценки процентного риска. Её можно применить к некоторым рядам, отражающим движение наличности, включая ренту, облигации и процентные свопы. Дюрация даёт точку отсчёта для сравнения двух или более инструментов. Она также используется для получения коэффициента хеджирования, проводимого в целях иммунизации портфеля.

Дюрация облигации есть средневзвешенное значение времени выплат по облигации. Она служит для измерения реакции цен на изменения доходности и может быть рассчитана по следующей формуле (Ф.Макоули) [7, стр. 15]:

,                                                                                                  (2.11)

где С_t - процентные выплаты за период t; t - период времени; T - срок погашения; r - доходность до погашения; Р - цена.

Дюрация облигации меньше номинального срока погашения последней или равна ему. Если платёж по облигации пред­ставляет собой процент и номинал, уплачиваемые в день её погаше­ния (например, облигация с нулевым купоном), то дюрация равна номинальному периоду погашения. Для любой купонной облигации (с периоди­ческими выплатами) дюрация всегда будет меньше, чем период времени до погашения Т.

Дюрация есть взвешенное время между покупкой ценной бума­ги и получением по ней прибыли, где в качестве весов использованы приведённые стоимости полученных выплат. Более низкая ценовая чувстви­тельность или дюрация характерны для инструментов с более высокими купонами, более высокой доходностью до погашения и бо­лее коротким сроком погашения. Напротив, более высокая ценовая чувствительность свойственна инструментам с низким купоном, низ­кой доходностью до погашения и длительным сроком погашения.

Эластичность процент­ной ставки представляет собой распространение традиционных кри­териев эластичности на изменения процентной ставки. Эластичность является мерой реакции цены инструмента на колебания процент­ных ставок [7, стр. 16]:

el = (dp/p)/(dr/r),                                                                                                     (2.12)

где р - цена инструмента, r - доходность, dp - изменение цены и dr - изменение доходности.

Поскольку dp и dr находятся в обратной зависимости, el будет меньше нуля. Высокие абсолютные значения el указывают на высокую способность цены инструмента реагировать на малые изменения процентных ставок. Высокая эластичность про­центной ставки свидетельствует о высокой степени процентного рис­ка, присущего данному инструменту.

Изменчивость курса облигации связана обратной зависимостью с процентной ставкой и прямой - со сроком погашения; поэтому оцен­ка процентного риска может быть сопряжена с трудностями, связан­ными с необходимостью учёта обоих этих факторов.

Между эластичностью и дюрацией существует зависимость [7, стр. 17]:

(-1)el=dur (r/(l+r)).                                                                                                 (2.13)

Можно также рассчитать систематический коэффициент процентной ставки путём разложения процентного риска на систематический (рынок) и несистематический (ценные бумаги) компоненты, на основе модели оценки стоимости активов, но наиболее полез­ным и удобным из трех методов оценки риска, указанных выше, является, по-видимому, метод дюрации, главным образом из-за отсутствия необходимости получения «исторических» данных.

На основе относительной дюрации, например, облигаций и фьючерсов на облигации можно получить тип коэффициента хеджи­рования, который может оказаться более достоверным, чем коэффи­циент, полученный на основе регрессионного анализа.

Коэффициент хеджирования   на основе дюрации, в частности, можно определить по следующей формуле [7, стр. 17]:

β_dur= (1 +r_c)(Р_s)(D_s)/[(1+r_s)(P_c)(D_c)],                                                                    (2.14)

где r_s - доходность до погашения облигации спот, Р_s - рыночная цена облигации, D_s - дюрация облигации, r_c - доходность до пога­шения стандартного фьючерсного контракта, P_c - рыночная цена стан­дартного фьючерсного контракта и D_c - дюрация стандартного фьючерсного контракта.

            Сочетание дюрации можно использовать не только для хеджирования облигаций посредством фьючерсов, но и для хеджирования процентных свопов посредством фьючерсов на облигации или облигациями в тех случаях, когда сроки погашения инструментов хеджирования и хеджируемых инструментов различаются.

            На практике в качестве меры курсовой изменчивости более часто используется модифицированная дюрация. Она определяется по следующей формуле [7, стр. 18]:

dur_m = dur /(1+y/f/100),                                                                                           (2.15)

где y –доходность в %, f – частота выплат за год.

Дюрация и модифицированная дюрация показывают, как изменится цена инструмента, если доходность или процентная ставка на рынке изменится на 1% или 100 базисных пунктов, но следует анализировать изменения цены и для очень малых изменений доходности. Многие участ­ники рынка для оценки изменчивости цены какого-либо инструмента используют приведённую стоимость базисного пункта (PVBP[6]), позволяющую проанализировать, какое влияние окажет изменение доходности или процентной ставки на рынке в один базисный пункт на цену каждого инструмента в портфеле.

Вторым важным применением PVBP является введение коэффициента хеджирования. Например, если имеется длинная позиция по одной облигации, то надо будет открыть короткую позицию по другой облигации в качестве хеджа, так чтобы компенсировать потерю по основной позиции равной при­былью по инструменту хеджирования. Определить, сколько облигаций требуется продать для компенсации любых потерь по длинной позиции, можно разделив PVBP длинной пози­ции на PVBP короткой позиции, что даст искомый коэффициент хеджирова­ния.

Процентный риск возникает, когда актив имеет большую дюрацию, чем пассив или горизонт планирования. Чем больше дис­пропорция, тем больше риск. Это отра­жается в ограничениях анализа с использованием дюрации. Пер­вое из них известно как «дрейф» дюрации. С течением времени портфель может стать более подверженным процентному риску, и дюрация хеджа может оказаться слишком большой. Следовательно, необходимо изменять структуру портфеля с течением време­ни и по мере осуществления платежей.

Другим ограничением является выпуклость[7]. Анализ с использованием дюрации является достаточным для очень малых изменений доходности, поскольку процентное изменение цены для одинакового увеличения или уменьшения доходности будет одним и тем же. Тем не менее, большие изменения кривой доходности снижают точность анализа с использованием дюрации, поскольку цена возрастает с увеличением ставки и уменьшается с уменьшением последней. За­висимость цена-доход является криволинейной. Зазор между каса­тельной к кривой доходности и самой этой кривой представляет со­бой ошибку, обусловленную выпуклость.

При изменении процентных ставок портфели, иммунизированные по дюрации, могут отличаться друг от друга. Например, две облигации могут иметь одну и ту же доходность и дюрацию, но по-разному реагировать на значительные изменения процентных ста­вок. Выпуклость можно использовать для определения коэффициента хеджиро­вания, поскольку длинная позиция по облигации имеет большую выпуклость, чем короткая.

В качестве эмпирических правил необходимо отметить следую­щие моменты:

-        при одинаковой дюрации бескупонные облигации имеют наименьшую, а облигации с большим купоном - наибольшую выпуклость;

-        при одинаковых сроках погашения бескупонные облигации име­ют наибольшую выпуклость;

-        увеличение дюрации на величину, превышающую едини­цу, увеличивает выпуклость на ещё большую величину;

-        с уменьшением доходности дюрация возрастает;

-         с увеличением доходности дюрация уменьшается.

2.4.       Портфельный подход к хеджированию

 

Основой портфельного подхода к хеджированию является комби­нирование стратегий снижения риска и максимизации прибыли. В подходах к хеджированию с точки зрения портфеля используются методы выбо­ра портфеля X. Марковица для выяснения, поче­му хеджеры должны быть держателями как хеджируемых, так и не хеджируемых инструментов или товаров.

Проблема хеджирования состоит, таким образом, в следующем:

Выбрать определенную фьючерсную позицию для формирования порт­феля с минимальным риском. Проблемы хеджеров соответствуют портфельному подходу. Если задана позиция, состоящая из Х_i натуральных единиц, присутствую­щих на рынке i, то хедж определяется как позиция из X_j единиц на рынке j, такая, что курсовой риск владения Х_i и X_j с момента времени t₁ по момент t₂ сводится к минимуму. Пусть, i представляет рынок спот, а j - рынок фьючерсов. Курсовой риск владе­ния Х_i может быть измерен вариацией изменения цены (σ_i); та же мера может быть использована для курсового риска X_j. Можно пока­зать, что общий курсовой риск портфеля, сформированного из активов двух видов Хi и Xj, равен дисперсии портфеля V(R) [5, стр. 26]:

V(R) = Х_i *σ_i + X_j *σ_j+2* Х_i * X_j*σ_i*σ_j*r_ij.                                                                 (2.16)

Поскольку цены по позиции спот и фьючерсной позиции часто будут изменяться в одном и том же направлении, то степень риска всей позиции будет зависеть от этой тенденции. Данное уравнение представляет собой математическую оценку степени риска общей позиции, то есть суммарной позиции спот и фьючерсной.

Целью стратегии хеджирования является минимизировать V(R). Для заданной позиции на рынке спот операция с X_j единиц на фьючерсном рынке сведёт риск к минимуму. Длинная позиция представляется положительными Х_i и X_j, а короткая - отрицательными, т. е. можно также сказать, следует ли покупать или продавать контракты на фьючерсных рынках. Если риск для i u j одинаков, σ_i = σ_j, и корреляция является совершенной, т. е. r_ij = 1. Однако для случая еврооблигаций и процентных фьючерсов есть вероятность, что отклонения движений цен будут различными, а корреляция будет менее совершенной, то есть r_ij < 1.