3. Управление рисками при помощи хеджирования на срочных рынках

3.1. Управление риском изменения процентной ставки

3.1.1.FRA

С развитием финансовой сферы в 60-е и 70-е годы банки получили возможность предлагать своим клиентам широкий спектр типов займов. В частности, распространённым способом финансирования стал среднесрочный заем, позволяющий клиентам занимать на срок до 7 или 10 лет вместо того, чтобы часто переоформлять краткосрочные займы. В свою очередь, банкам пришлось обеспечивать себе краткосрочное финансирование с помощью розничных депозитов или депозитов денежного рынка. Это не составляло для них проблемы, поскольку одну из традиционно приписываемых банку ролей составляют краткосрочный заем и долгосрочный кредит - так называемая функция трансформации сроков погашения. Банки не особенно сомневались в своей способности конвертировать сроки погашения, так как, за исключением глобальных банковских кризисов, они могли при необходимости привлекать средства с рынка, хотя бы за счёт увеличения процентной ставки.  Однако банки не могли фиксировать заранее процентную ставку для привлекаемой таким образом наличности. Им приходилось выплачивать меняющуюся по времени ставку и затем перекладывать эти выплаты на заёмщиков. Таким образом, среднесрочные кредиты могли гарантировать финансирование, но не ставку, по которой оно предоставлялось.  Когда в 70-х и начале 80-х годов волатильность процентных ставок увеличилась, казначеи корпораций стали требовать у банков средства защиты от риска увеличения стоимости кредита. Банки предложили частичное решение этого вопроса в виде форвард-форвардного (или срочно-срочного) займа, названного так потому, что даты получения кредита и его погашения относились к будущему.

Форвард-форвардные займы пользовались спросом в 70-е годы, но не были удобными для банков, поскольку им приходилось делать заем на полный срок — со дня сделки до завершающего погашения форвард-форвардного займа. Взятие займа занимает кредитную линию и капитал, которые являются ограниченными и дорогими ресурсами.  Наибольший ущерб банковской прибыли создаёт то, что банку для поддержания балансового отчёта необходимо резервировать капитал в течение длительного периода. Условия резервирования капитала вводятся центральными банками по весьма серьёзной причине: они подстраховывают банки в случае невозврата кредитов. Задача устранения форвард-форвардных займов из балансового отчёта решается при помощи FRA[8].

Почти все реально заключаемые FRA удовлетворяют стандартным условиям, выработанным Ассоциацией британских банкиров (ВВА) в 1985 г., так называемым условиям FRABBA.

Кроме установления порядка заключения соглашений, этот документ определяет ряд важных терминов:

-        контрактная сумма[9] - размер основного капитала, который условно занимается или отдаётся в кредит,

-        контрактная валюта[10] - валюта, в которой выражена контрактная сумма,

-        дата сделки[11]  - день заключения FRA,

-        расчётная дата[12] - начальный день условного кредита или депозита,

-        дата фиксации[13] - день определения ставки-ориентира,

-        дата погашения[14] - день погашения условного кредита или депозита,

-        срок контракта[15] - число дней между расчётной датой и датой погашения,

-        контрактная ставка[16] - зафиксированная условиями FRA процентная ставка,

-        ставка-ориентир[17] - рыночная процентная ставка, используемая в дату фиксации для определения расчётной суммы,

-        расчётная сумма[18] - вычисляемая по разности между контрактной ставкой и ставкой-ориентиром сумма, которую в расчётную дату одна сторона платит другой.

Для обычных займов или депозитов в европейской валюте ставка фиксируется в день сделки, но основной капитал не меняет владельца до даты валютирования (обычно в течение двух рабочих дней). Это правило действует и в FRA. Начальным днём условного займа или депозита считается расчётная дата, но ставка определяется двумя днями раньше, в дату фиксации.    Как правило, ставка-ориентир — это ставка LIBOR в дату фиксации. Покупатель в FRA является поэтому условным заёмщиком и защищён от увеличения процентной ставки, однако он должен будет платить, если ставки упадут. Покупатель может иметь реальные долговые обязательства и использовать FRA для хеджирования.

Продавец FRA является условным кредитором и фиксирует ставку для кредитования или инвестирования. Продавец FRA поэтому защищён от падения процентных ставок, но должен платить, если ставки поднимаются. Продавец может быть инвестором, который рискует пострадать в случае падения ставок, но может также, не будучи инвестором или кредитором, надеяться получить доход от падения процентных ставок.  По условиям FRA никаких реальных ссуд или займов не делается. Одна или обе стороны FRA могут иметь долговые или инвестиционные обязательства, но они должны быть оформлены отдельными соглашениями. FRA лишь обеспечивает защиту от изменения процентных ставок. Эта защита проявляется в виде выплаты наличными расчётной суммы, которая компенсирует каждой стороне разницу между процентной ставкой, установленной условиями FRA, и ставкой, складывающейся на рынке к моменту окончания FRA.

По сути, FRA — это форвард-форвардная ссуда с фиксированной процентной ставкой, но без фактического кредитного обязательства. Поскольку по условиям FRA ссудная сумма не перечисляется, этот инструмент не отражается в балансовых отчётах и устраняет необходимость резервирования капитала, лишавшую привлекательности форвард-форвардные займы. Хотя некоторые требования по резервированию банками капитала для покрытия FRA остаются, соответствующая сумма составляет всего около одной сотой от требуемой для форвард-форвардного займа.

FRA является внебиржевым продуктом, предлагаемым банками. Как и рынок иностранной валюты, рынок FRA является глобальным рынком, созданным банками.

Ставку FRA i_F можно рассчитать по следующей формуле [6, стр. 48]:

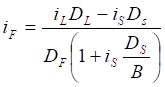,                                                                                    (3.1)

где Ds - число дней от спот-даты до расчётной даты, D_L - число дней от спот-даты до даты погашения, D_F - число дней периода контракта, В - условное число дней в году, i_L - рыночная процентная ставка при инвестициях до даты погашения, i_S - рыночная процентная ставка при инвестициях до расчётной даты.

Расчётная сумма по FRA обычно выплачивается в расчётную дату, т.е. в начальный день займа или депозита. Поскольку эта сумма выплачивается раньше, чем необходимо, она может быть размещена для получения дохода. Для учёта этой возможности расчётную сумму уменьшают на величину дохода, который мог бы быть получен при размещении расчётной суммы с расчётной даты до даты погашения. Стандартную формулу вычисления расчётной суммы можно записать в следующем виде [6, стр. 43]:

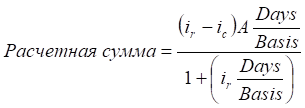,                                                        (3.2)

где i_r - ставка-ориентир, i_c  - контрактная процентная ставка, A - контрактная сумма, Days - срок контракта, Basis - условное число дней в году.

            Если риск процентной ставки привязан к LIBOR, а покрываемый период точно совпадает с датами одного из стандартных контрактов, то FRA может обеспечить совершенный или почти совершенный хедж. Если возникает неувязка между периодом риска и периодом, покрываемым стандартным контрактом FRA, то пользователь располагает тремя возможностями:

1.     Получить от банка индивидуальную котировку, но нестандартный FRA хотя и может привести к почти совершенному хеджу, будет иметь более высокую стоимость.

2.     Хеджировать ближайшими стандартными FRA-контрактами, смирившись с остаточным базисным риском.

3.     Хеджировать стандартными FRA, но управлять базисным риском.

3.1.2.  Процентные фьючерсы

 

Одно из ключевых различий между FRA и фьючерсами состоит в гибкости первых по сравнению со стандартизацией вторых. Но практически все проблемы, за исключением проблемы расхождения даты прекращения риска и даты гашения фьючерса, которую можно минимизировать, но нельзя исключить полностью, могут быть разрешены за счёт правильного расчёта коэффициента фьючерсного хеджирования.

За счёт подбора подходящих множителей с помощью коэффициента хеджирования можно компенсировать: риск основного капитала, срок действия риска, базисный риск, расчётную сумму, маржинальные потоки.

Коэффициент хеджирования рассчитывают, как произведение влияния вышеуказанных составляющих [6, стр. 441-445].

HR=HR_basic*HR_advanced,                                                                                             (3.3)

где

HR_basic=HR_principal*HR_period,                                                                                      (3.4)

HR_advanced=HR_exbasic*HR_settlement*HR_margin,                                                                (3.5)

HR_principal, HR_period, HR_exbasic, HR_settlement, HR_margin – составляющие коэффициента хеджирования, учитывающие соответственно риск основного капитала, срок действия риска, базисный риск, расчётную сумму, маржинальные потоки.

,               (3.6)

,                         (3.7)

,                                                                                                            (3.8)

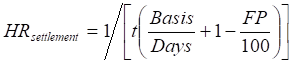,                                                                       (3.9)

где t – номинальный срок фьючерсного контракта (в годах), Basis – условное число дней в году, Days – реальное число дней в периоде действия фьючерса, FP – текущая цена фьючерса, β – коэффициент регрессии.

Если планируется фьючерсный контракт закрыть досрочно, то используется следующая формула [6, стр. 445]: 

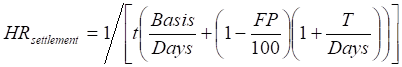,                                                 (3.10)

где T – число дней до даты погашения от момента закрытия фьючерсной позиции.

Поток вариационной маржи можно определить по следующей формуле [6, стр. 447]:

,                                                                        (3.11)

где суммарная вариационная маржа, выплачиваемая или получаемая, без учёта процентных начислений VM_total = N*(F_T-F₀)*TV, N – число фьючерсных контрактов, F₀ – начальная цена фьючерса, F_T - цена фьючерса в момент погашения или ликвидации, TV – контрактное значение тика, D_H – число дней в периоде хеджирования. Допущение – считаем, что стоимость фьючерса меняется линейно от F₀ до F_T.

При данных условиях верно следующее выражение [6, стр.447]:

.                                                                                 (3.12)

Как правило, используют стек-хеджирование, используя пакет фьючерсов с одинаковой датой погашения, являющейся ближайшей датой, следующей за датой фиксации ставки по основному риску, или стрип-хеджирование, используя последовательность фьючерсных контрактов, также с датами исполнения, последующими за датой фиксации ставки по основному риску. Если запланировано закрытие хеджа до наступления срока исполнения фьючерсных контрактов, то возникает базисный риск, связанный с изменениями формы кривой доходности. Управлять данными рисками можно с помощью спрэд-хеджа. Число контрактов, необходимых для минимизации базиса сближения составляет [6, стр. 459]:

,                                                                                           (3.13)

где N_spread – число контрактов в хедже, N_basic – число контрактов в базисном фьючерсном хедже, t_prior – промежуток времени между ликвидацией хеджа и датой погашения фьючерса, t_contract – промежуток времени, покрываемый фьючерсным контрактом.

3.1.3.  Использование свопов

 

FRA и фьючерсы годятся для управления риском по единичной срочной ставке. Процентный своп позволяет управлять риском по множеству процентных периодов в будущем. Применение свопов можно разделить на два класса: свопы, связанные с активами, используются для изменения характеристик потока доходов инвесторов, свопы, связанные с пассивами, используются для изменения потоков денежных средств заёмщика.

Пассив-свопы:

-        От плавающей к фиксированной. Заключается в переводе заёмных обязательств по плавающей ставке в обязательства по фиксированной.

-        От фиксированной к плавающей. Обратный случай.

-        От фиксированной через плавающую к фиксированной. По существу является комбинацией свопов.

-        Межвалютный от плавающей к плавающей. Используется в случае возможности заимствования на дешёвых рынках.

Актив-свопы являются зеркальным отражением пассив-свопов. Возможности конструирования свопов практически безграничны, и почти любую характеристику свопа можно подогнать к конкретным запросам.

3.1.4.  Опционы

 

Опцион на FRA обычно называют гарантией процентной ставки (IRG[19]). Он позволяет его владельцу выбирать между определенной процентной ставкой и текущей процентной ставкой в некоторый момент времени.

Процентный кэп[20] представляет собой специализированный продукт, эквивалентный набору опционов[21]. Для определения цены кэплетов (отдельных опционов в составе кэпа) можно использовать, например модель Блэка-Шоулса [6, стр. 340]:

,                                                                     (3.14)

, ,        

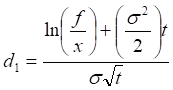где CAPLET – премия за кэплет, в процентах от суммы займа, T – продолжительность защищаемого периода, t – продолжительность времени ожидания, z – непрерывно начисляемая ставка по нулевым купонам в период ожидания, f – форвардная ставка для защищаемого периода, x – ставка исполнения по кэпу, N () – функция стандартного нормального распределения, σ – волатильность форвардной процентной ставки.

            Контракт флор эквивалентен набору пут-опционов, комбинация из продажи флора с меньшей ставкой исполнения и покупки кэпа с большей ставкой исполнения называется коллар. Возможность для защиты процентной ставки на длительные сроки предоставляет свопцион[22] - опцион на право вступить в процентный своп в определенный день в будущем.

            Стоимость свопциона можно определить по следующим формулам [6, стр. 347]:

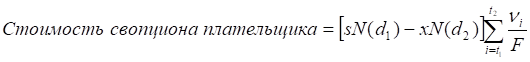,                       (3.15)

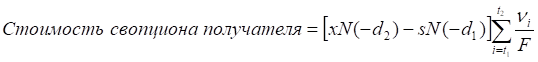,                      (3.16)

где s – текущая ставка по отсроченному свопу, x – ставка исполнения опциона, ν_i – дисконтирующий множитель для конца i-го периода, считая от сегодняшнего дня, t₁ – номер периода, когда начинается действие отсроченного свопа, t₂ – номер периода, когда заканчивается действие отсроченного свопа, F – число купонных выплат в год.

  Существуют также так называемые сложные опционы: кэпцион, флорцион и колларцион, которые дают право купить соответствующий основной опцион, а также большое количество экзотических опционов, которые могут быть темой для отдельной работы, и в настоящей освещены будут частично.

Приведённые методы управления рисками изменения процентной ставки банки стараются использовать, не выходя на открытый рынок, предпочитая формировать свою систему активов и пассивов уравновешенной, так как это позволяет не нести дополнительных расходов. При управлении риском изменения процентной ставки банки применяют интегральный метод управления рисками. Все процентные риски объединяются, и осуществляется управление единым риском. При проведении внутренней оценки финансовых результатов по направлениям работы, подразделениям, отдельным инструментам, а также при планировании новых операций, могут быть использованы вышеуказанные методы, позволяющие минимизировать процентные риски, либо получать доходы от управления ими, но операции рассматриваются опять же не отдельно, а по отношению к имеющейся в банке ситуации.

 

3.2.       Управление валютным риском

 

3.2.1.  Инструменты с наличными

 

        К инструментам с наличными относят все традиционные средства валютного рынка, например – форвардные сделки, которые устанавливает курс обмена согласованного количества валюты на определенную дату в будущем, либо в любой момент определенного интервала времени в будущем, или валютный своп, который позволяет зафиксировать курсы обмена валют в согласованную дату с их обратным обменом при наступлении другой согласованной даты. Большое преимущество таких инструментов состоит в том, что все детали сделки могут быть точно согласованы сторонами.

Зная сегодняшние рыночные ставки, дилер может найти цену форвардного обмена валюты, не имея информации о будущем значении спот-курса. В этом и состоит сущность оценивания при помощи безрискового арбитража.  Можно вывести простую формулу для оценивания форвардного курса обмена валюты (эта формула относится к расчётам форвардных курсов на срок до одного года. Для долгосрочных сделок обмена валюты формулу нужно изменить, чтобы она учитывала сложные проценты):

 

F=S x [1+(i_q*Days/Basis_q)] / [1+(i_b*Days/Basis_b],                                                (3.17)

 

где F - форвардный (срочный) курс обмена валюты, S - текущий валютный спот-курс, i_q -процентная ставка по котируемой валюте,  i_b - процентная ставка по основной валюте, Days - число дней от спот-даты до форвардной даты, Basis_q - число дней в году, установленное для расчётов в котируемой валюте, Basis_b - число дней в году, установленное для расчётов в основной валюте и все процентные ставки выражаются десятичными дробями.

Практически на валютном рынке форвардные валютные курсы котируются не в абсолютных цифрах, а в виде разности между спот- и форвардным курсами (как форвардная маржа, или своп-пункты). Так делают потому, что форвардный курс очень чувствителен к изменениям спот-курса и почти точно повторяет его колебания. Дилеру форвардных обменов валюты приходилось бы изменять котировки при любом, даже незначительном, изменении спот-курса. Своп-пункты, с другой стороны, очень слабо зависят от своп-курса и котировок и поэтому значительно более устойчивы. Следующая формула позволяет вычислять своп-пункты:

W=S * ([1+(i_q * Days/Basis_q)] / [1+(i_b * Days/Basis_b] - 1),                                  (3.18)

где W- форвардная маржа, или своп-пункты, а все остальные символы имеют тот же смысл, что и раньше. 

3.2.2.  Валютные фьючерсы

 

Рынок финансовых фьючерсов в целом неизменно растет в течение всех лет своего существования. Конкуренция между разными биржами порождает непрерывный прогресс, как в разнообразии предлагаемых контрактов, так и в организации торговли. Уникальной чертой фьючерсного рынка является “прозрачность”, основанная на том, что все действия на нем совершаются открыто. Все происходит на глазах у всех при тщательном контроле со стороны руководства биржи. Все могут видеть соотношение между рыночным спросом и предложением, которое выражается в относительной численности покупателей и продавцов.

Этот порядок, принятый фьючерсных биржах, гарантирует очень маленький разрыв между ценами предложения и спроса — обычно 1 или 2 тика. Кроме этого, всегда есть уверенность в том, что сделка совершена по наилучшей возможной в тот момент цене. Требование открытости вместе с контролем со стороны руководства биржи позволяет предотвратить внерыночные сделки или сделки, использующие конфиденциальную информацию.

Внебиржевой рынок предоставляет большую свободу в выборе условий контрактов. Почти любой параметр внебиржевой сделки может быть предметом обсуждения, и ее условия могут быть приспособлены к специфическим потребностям сторон. Напротив, фьючерсные контракты полностью стандартизованы. Лежащий в основе контракта финансовый инструмент, даты поставки, другие технические детали — все это заранее определено. При совершении фьючерсной сделки остаётся согласовать только две вещи: число покупаемых (продаваемых) контрактов и цену. Подчинение фьючерсного рынка строгим стандартам вынуждает участника сделки идти на определенный компромисс: фьючерсный контракт, который он покупает или продаёт, может не полностью соответствовать его потребностям. Большие объем и частота совершения сделок предопределяют успешную работу фьючерсного рынка.

Важным преимуществом проведения сделок на фьючерсных биржах является использование клирингового механизма, так как члены биржи переносят риск, идущий от партнёра по сделке, на клиринговую палату. Однако если взять весь объем фьючерсных сделок, то станет ясно, что общий размер риска огромен. Клиринговая палата не может позволить себе брать на себя весь этот риск, не приняв никаких мер для защиты своего финансового положения на случай невыполнения обязательств кем-либо из членов. Такая защита осуществляется системой выплаты маржи.

Фьючерсная маржа действует как облигация с гарантией от невыполнения обязательств эмитентом (performance bond). Она защищает клиринговую палату от потерь в случае неплатёжеспособности члена биржи. Когда участник торгов закрывает свою позицию, маржа погашается.

Важнейшей частью системы маржинальных расчётов, которая, собственно, и делает систему работоспособной, является ежедневная переоценка с учётом изменения цен рынка (marking-to-market). Ежедневно, сразу после окончания торгов, фьючерсная биржа публикует расчётные цены - официальные цены закрытия на этот день. Каждая незакрытая позиция переоценивается относительно расчётной цены. Потери, возникшие вследствие изменения расчётной цены за день (или от разницы между расчётной ценой и ценой сделки, если та была заключена в этот день), заносятся на маржинальный счёт члена биржи и должны быть уплачены наличными на следующий день утром. Все доходы также заносятся на счёт и могут быть получены на следующий день. Таким образом, возникают два вида маржи: начальная, которая вносится при занятии позиции, и вариационная, которая, в зависимости от результатов переоценки по текущим ценам, может оказаться положительной или отрицательной. В соответствии с этой ежедневной процедурой маржинальные счета обновляются после каждых торгов. В результате потенциальные потери будут ограничены изменением рыночной цены, которое может произойти за один день, а не за весь срок действия контракта.

Вариационная маржа подсчитывается в конце каждого дня торгов, исходя из вечерней расчётной цены этого дня, и обычно подлежит выплате к определенному часу утром следующего дня. В тех редких случаях, когда член биржи оказывается не в состоянии внести требуемую вариационную маржу, биржа имеет право ликвидировать фьючерсную позицию, возместить все свои убытки, сняв нужную сумму с маржинального счета, и вернуть остаток. Клиринговая палата понесёт убытки только в том случае, если дневное изменение цены превысит сумму, находящуюся на маржинальном счёте. Тогда потери будут возмещены из специального общего фонда, который содержится на взносы всех членов биржи. Биржа обычно назначает уменьшенную маржу для составной позиции. Такая уменьшенная маржа называется спрэд-маржой или стрэддл-маржой.  

На ряде бирж, особенно в США, принята двухуровневая система маржи. Вводится ещё один уровень маржи - поддерживающая маржа[23], - который обычно устанавливается в размере 3/4 от начальной маржи. При первоначальном занятии позиции член биржи должен внести начальную маржу в обычном порядке. Однако требования по выплате маржи могут возникнуть только тогда, когда сумма на маржинальном счёте окажется ниже поддерживающей маржи - лишь в этом случае член биржи должен восстановить баланс до уровня начальной маржи. Таким образом, биржа не настаивает на том, чтобы сумма на маржинальном счёте поддерживалась на уровне начальной маржи, а допускает колебания этой суммы в пределах от поддерживающей до начальной маржи. Такой порядок во много раз уменьшает число маржинальных платежей, которые приходится производить членам биржи (особенно, в случае колебаний фьючерсных цен), и поэтому сокращает организационные расходы.

Наряду с указанными преимуществами, фьючерсный рынок накладывает определенные ограничения. Находясь перед выбором, что в большей степени отвечает поставленным целям: фьючерсный контракт или соответствующий внебиржевой инструмент, следует взвесить все эти преимущества и ограничения. При сделках на внебиржевом рынке клиенты и банки вправе выяснять степень состоятельности другой стороны. Довольно часто случается так, что потенциальная сделка отменяется из-за того, что одна из сторон оценивает риск, происходящий от другой стороны, как недопустимо высокий. Впрочем, в случае явно неравнозначного финансового положения контрагентов, стороны вполне могут договориться о том, что менее «надёжная» сторона в качестве обеспечения по сделке разместит маржу у более «надёжной» стороны.

На фьючерсном рынке нет смысла опасаться риска от другой стороны. При заключении сделки вообще нет нужды интересоваться тем, что представляет собой другая сторона: кто бы это ни был, его место тотчас же займёт клиринговая палата. Конечно, это не устраняет риск совершенно, а переносит его со всего множества возможных партнёров на одного конкретного — клиринговую палату. Однако фьючерсные биржи гарантируют, что их клиринговые палаты платёжеспособны и вне подозрений, насколько это вообще возможно. Надо признать, что факты неплатёжеспособности клиринговых палат немногочисленны, характерны для развивающихся рынков и в периоды острейших кризисов.

Хеджирование фьючерсным контрактом заключается в открытии временной позиции на фьючерсном рынке, которая близка по параметрам и противоположна по сути позиции инвестора на наличном рынке и защищает его от рыночного риска. Хеджирование основывается на предположении о близком к параллельному движениям наличной цены базисного актива и фьючерсной цены. Любая попытка уменьшить риск потерь с помощью хеджирования фьючерсными контрактами должна принимать во внимание отношение наличной цены базисного актива к фьючерсной цене, определяющее прибыль или убытки от хеджа.

Валютные фьючерсы служат удобным инструментом страхования для банков, пенсионных фондов и других финансовых институтов по сравнению с альтернативными способами хеджирования. В настоящее время существует возможность открытия и закрытия фьючерсных позиций на биржах разных стран мира. Этот «взаимный зачёт» очень привлекателен для многих многонациональных организаций, которые используют фьючерсные сделки для ограничения риска на всемирной основе. Выигрыши/потери инвестора при хеджировании фьючерсным контрактом характеризуются базисным риском, то есть риском, связанным с разницей между наличной ценой базисного актива и фьючерсной ценой в момент окончания хеджирования.

Традиционно имеются два существенных соображения при решении вопроса о том, какой фьючерсный контракт лучше всего подходит для хеджирования в конкретной ситуации — это соотношение между базисным риском и ликвидностью. Пользование контрактами, предлагающими достаточную ликвидность, может приводить к недопустимому базисному риску и наоборот.

К хеджированию продажей фьючерсного контракта пользователь прибегает, если в будущем планирует продать некоторый актив, которым он владеет в настоящее время или собирается его вскоре получить и хеджирование защищает от возможного падения цены актива. Если пользователь собирается в будущем приобрести какой-либо актив, он использует хеджирование покупкой фьючерсного контракта и хеджирование защищает от роста цены актива.

Обычно открытые фьючерсные позиции закрываются путём офсетной сделки до даты поставки, так как большинство страхующихся при приближении этой даты теряет необходимость в страховании, а торговля их базисными активами производится на спотовом (наличном) рынке.

На практике хеджирование посредством фьючерсного контракта из-за его сильной стандартизации не всегда может полностью исключить риск потерь, так как актив, торгуемый на спотовом рынке, может несколько отличаться от предмета фьючерсного контракта, и сроки фьючерсного контракта могут не полностью соответствовать срокам купли-продажи актива на спотовом рынке.

Необходимость хеджирования от валютного риска в последнее время связана с включением в многие портфели иностранных ценных бумаг. Хеджирование валютными фьючерсами часто используется для страхования процентного арбитража от валютного риска.

Покрытие валютного риска для процентных арбитражных операций считается делом сложным и дорогостоящим и заключается в обратном обмене валюты по фиксированному форвардному курсу, например, посредством валютного фьючерса. Расчёты в покрытом процентном арбитраже заключаются в определении по двум переменным третьей, где переменными являются две безрисковые процентные ставки на каждую валюту, а также соотношение между двумя валютными курсами, по одному на каждый срок поставки.

 Процентный арбитраж с фьючерсным покрытием в рамках двух валют включает в себя следующие операции:

- перевод первой валюты во вторую по спот-курсу 1/S₀:

;                                                                                                              (3.19)

- продажу K_f  валютных фьючерсных контрактов размера M_f по цене S_T^f;

- хранение второй валюты на депозите:

;                                                                                         (3.20)

- получение арбитражёром второй валюты по окончании срока депозита;

- закрытие фьючерсных позиций при расчётной цене S_T;

- продажа второй валюты за первую по курсу S_T:

.                                                                                                            (3.21)

Здесь предполагается, что срок депозита и срок до поставки фьючерсного контракта совпадают. На практике очень сложно полностью закрыть арбитраж с использованием фьючерсных контрактов из-за их высокой стандартизации.

По большому счету арбитражёры не заинтересованы в физической поставке и стремятся закрыть позиции офсетными сделками по мере того, как рыночная ситуация позволит им реализовать свою прибыль подобным путём. Закрытие фьючерсной позиции должно сопровождаться новыми компенсирующими сделками на рынке наличности, чтобы сохранить прибыль от арбитража до наступления срока расчётов по первоначальным сделкам, что опять потребует расходов. Прибыли/убытки, полученные арбитражёром по окончании хеджируемой финансовой операции, вычисляются по формуле:

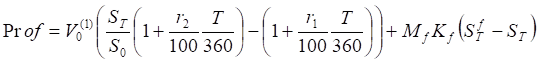,                      (3.22)

где S_t - текущая цена единицы актива, F_t - текущая фьючерсная цена, T_s - срок продажи актива на спот-рынке, M_s - размер актива, M_f - размер фьючерсного контракта, K_f - число проданных фьючерсных контрактов.

Допустим, пользователь планирует в будущий момент времени продать некоторый актив и хочет застраховаться от падения его цены, продав соответствующее число фьючерсных контрактов на этот базисный актив по текущей фьючерсной цене. Начальные убытки пользователя составляют только комиссионные брокеру за продажу фьючерсных контрактов, а наличный базисный актив может использоваться в качестве маржи.

В этом хедже прибыли/убытки инвестора определяются по формуле:

.                                                                (3.23)

Формула (3.23) включает в себя базисный риск  и риск, связанный с неполным покрытием хеджированием всей стоимости актива.

3.2.3.  SAFE

 

Согласно уравнению расчёта форвардного курса своп-сделки обмена валют, своп-курсы зависят, главным образом, от разностей процентных ставок по этим двум валютам. Разумеется, именно разница между курсом спот и форвардным обусловливается, в первую очередь, разницей между процентными ставками. Сравним это с форвард-форвардным депозитом. Хотя в своё время он обычно использовался для хеджирования, также можно было применять и при игре на процентных ставках. К сожалению, форвард-форвардный депозит связан с реальными потоками наличности, а следовательно, с необходимостью резервирования капитала. То же самое верно и для форвард-форвардного свопа обмена валюты, позволяющего использовать изменения разницы между процентными ставками, но также связанного с реальными потоками наличности и резервированием капитала. Это неудобство устраняет SAFE - составное соглашение о будущем обмене[24].

SAFE — это внебалансовый форвард-форвардный своп обмена валюты, или иными словами - соглашение, заключённое двумя сторонами с целью либо хеджировать, либо спекулировать на изменениях разности между процентными ставками или спрэда свопов обмена валюты.

SAFE использует, главным образом, разности между процентными ставками, а не их абсолютные значения. SAFE появились в конце 1980-х годов и, как и FRA, являются внебиржевым продуктом. Для любых пар основных валют SAFE могут заключаться со стандартными сроками погашения от 1 до 12 месяцев; допустимы также и нестандартные сроки. Будучи несколько специфичнее FRA, SAFE предлагаются более узким кругом банков, и поэтому их ликвидность значительно ниже.

Две стороны в SAFE соглашаются провести форвард-форвардный своп обмена двух валют. Одна валюта называется первичной, а другая - вторичной. Эти валюты будут условно обменены в один и тот же будущий день - расчётную дату[25] - и условно обменены в обратном направлении в день погашения[26]. Как правило, по условиям SAFE количество первичной валюты, условно обмениваемой в оба этих дня, одно и то же, однако возможен и вариант с двумя разными количествами первичной валюты.

Покупатель SAFE — это тот, кто условно покупает первичную валюту в расчётную дату и продаёт её при погашении. Продавец в SAFE занимает противоположную позицию. Как и для FRA, термины «покупатель» и «продавец» относятся только к направлениям условных потоков наличности, а не к инициатору сделки. Никаких обменов основного капитала в действительности не происходит. Когда две стороны договариваются заключить SAFE, они согласовывают обменные курсы, по которым будут проводиться условные сделки. В расчётную дату одна сторона выплачивает другой расчётную сумму, вычисленную по разнице между ставками в условиях соглашения и текущими ставками в этот день.

Термины для SAFE определены в положении SAFEBBA, опубликованном Ассоциацией британских банкиров. Основными терминами[27] являются: А1 - первая контрактная сумма, А2 - вторая контрактная сумма, OER[28] - договорный обменный курс, CFS[29] - спрэд форвардного контракта, SSR[30] - расчётный спот-курс, SFS[31] - расчётный форвардный спрэд. Расчётная дата и дата погашения имеют тот же смысл, что и в FRA. Окончательный результат SAFE определяется в дату фиксации, обычно за два дня до расчётной даты.

В день сделки стороны должны договориться об условных суммах первичной валюты, A1 и А2, которые подлежат обмену в расчётную дату и в дату погашения, соответственно. Обычно эти суммы одинаковы. Стороны должны также согласовать OER и CFS. Тем самым фиксируются договорные обменные курсы в расчётную дату и в дату погашения, что позволяет рассчитать условные суммы вторичной валюты.

В день фиксации SSR и SFS определяются аналогично LIBOR по котировкам банков из некоторого списка, причём при вычислении средней величины наименьшее и наибольшее значения исключаются. Курсы SSR и SFS публикуются в Reuters.

Расчётная сумма по SAFE вычисляется путём сравнения обменных курсов, установленных соглашением для расчётной даты и даты погашения, именно, OER и CFS, со значениями текущих курсов в эти дни.

Термин SAFE объединяет целое семейство составных соглашений по обмену валюты, из которых наиболее распространёнными являются:

ERA[32] - соглашение об обменном курсе,

FXA[33] - соглашение о форвардном обмене.

Они различаются только способом вычисления расчётной суммы, однако это изменяет природу предоставляемой защиты. ERA задаёт только разность между своп-пунктами, зафиксированными в соглашении, и своп-пунктами, складывающимися к моменту погашения. Таким образом, расчётная сумма зависит от эволюции только одной переменной - своп-пунктов - в интервале между расчётной датой и датой погашения. FXA относится не только к своп-пунктам за период контракта, но также к любым изменениям абсолютного уровня обменных курсов. Другими словами, FXA отслеживает не только любое различие между CFS и SFS, но и любое различие между OER и SSR.

Какой контракт использовать - зависит от того, для чего он применяется. Тот, кто хочет хеджировать стоимость обычных свопов обмена валюты, предпочтёт FXA, так как выплаты по нему точнее соответствуют защищаемому риску. Тому же, для кого опасны только изменения разностей процентных ставок, следует предпочесть ERA, устраняющее большую часть зависимости от колебаний валютных курсов.

Расчётная сумма для ERA вычисляется по формуле [6, стр. 63]:

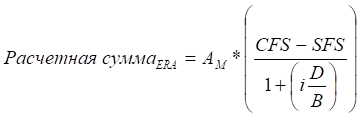.                                                         (3.24)

Расчётная сумма для FXA вычисляется по формуле:

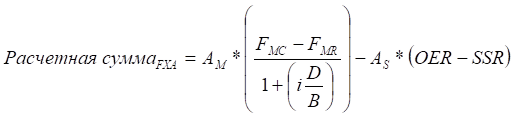,                           (3.25)

где As - условная сумма первичной валюты, обмениваемая в расчётную дату, A_M- условная сумма первичной валюты, оцениваемая в дату погашения, OER - зафиксированный в контракте форвардный курс для расчётной даты, SSR - форвардный курс для расчётной даты, определенный в дату фиксации, F_MC - зафиксированный в контракте форвардный курс для даты погашения, F_MR - форвардный курс для даты погашения, определенный в дату фиксации, CFS - зафиксированные в контракте своп-пункты за период контракта, SFS - своп-пункты за период контракта, определенные в дату фиксации, i - процентная ставка по вторичной валюте, D - число дней в контрактном периоде, B - условное число дней в году для расчётов по вторичной валюте, F_MC= OER+CFS, F_MR=SSR+SFS.

Как для ERA, так и для FXA условные суммы определяются в первичной валюте, а расчётные суммы - во вторичной. Это соответствует соглашениям, принятым на спот-рынке. Например, дилер, покупающий и продающий равные суммы долларов против немецких марок, будет торговать долларами («первичной валютой»), а получать прибыли или убытки в немецких марках (во «вторичной валюте»). Формулы расчётной суммы определяют стоимость SAFE для покупателя, позиция которого в SAFE называется «длинной». Положительный результат означает, что продавец платит покупателю, а отрицательный - что покупатель платит продавцу.

Ценообразование в системе SAFE основано на том, что справедливая цена должна быть выбрана так, чтобы ожидаемое значение расчётной суммы было равно нулю. Определенная соотношением для ERA расчётная сумма зависит от разности между установленными контрактом своп-пунктами CFS и рыночными своп-пунктами SFS на дату фиксации. Оценивание ERA означает такой выбор CFS в день сделки, чтобы ожидаемое значение расчётной суммы было равно нулю. Можно записать это условие следующим образом:

Е (расчётная сумма) = 0 , т.е. CFS = Е (SFS ),                                                  (3.26)

где Е( ) - оператор математического ожидания.

Иными словами, цена ERA в день сделки должна равняться математическому ожиданию своп-пунктов в дату фиксации. Согласно уравнению форвардной маржи (3.18) своп-пункты определяются тремя переменными: спот-курсом, процентной ставкой в котируемой валюте i_q и процентной ставкой в базовой валюте i_b.

 Чтобы найти (приближенное) математическое ожидание своп-пунктов в какую-либо будущую дату, нужно заменить значения этих трех переменных их математическими ожиданиями. Эти математические ожидания - не что иное, как форвардные ставки.

Из уравнения форвардной маржи (3.18) следует, что:

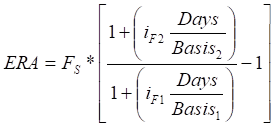,                                                                         (3.27)

где ERA - справедливая рыночная цена для ERA, Fs - форвардный курс в расчётную дату, i_F1 - ставка FRA по первичной валюте на период ERA, i_F2 - ставка FRA по вторичной валюте на период ERA, Days - число дней контрактного периода, Basis₁ - число дней в году для расчётов в первичной валюте, Basis₂ - число дней в году для расчётов во вторичной валюте, все процентные ставки выражаются десятичными дробями. 

Формулу (3.27) можно также записать в следующем виде для справедливого форвардного курса Fs:

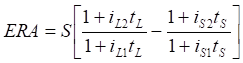,                                                                                  (3.28)

,

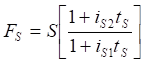где S - текущий курс спот, i_S1, i_S2 - процентные ставки рынка наличности на срок до расчётной даты по первичной и вторичной валютам, i_L1, i_L2 - процентные ставки рынка наличности на срок до даты погашения по первичной и вторичной валютам, t_S - время от спот-даты до расчётной даты, t_L - время от спот-даты до даты погашения, t_F -  длина контрактного периода.

3.2.4.  Опционы

 

Общее свойство всех решений, указанных выше состоит в том, что они позволяют пользователю зафиксировать на будущее обменный курс валют. Это устраняет неопределённость и, следовательно, риск, связанный с волатильностью спот-курсов. Однако фиксация курса устраняет не только риск потерь, но и возможность выгадать от благоприятных изменений спот-курса. Чтобы получить такую возможность, сохраняя защиту от неблагоприятных колебаний, необходимо использовать методы, основанные на опционах. Валютный опцион обеспечивает покупателя опциона правом покупать или продавать иностранную валюту в определенный день или в течение определенного времени по фиксированному курсу. Валюта, в которой реализуется премия и цена исполнения опциона называется валютой торговли, а валюта, которая покупается или продаётся, называется базисной валютой.

В сделках с опционами основной риск несут подписчики опционов, так как их прибыль всегда ограничена величиной премии, а возможные убытки при неблагоприятном движении цены базисного актива не ограничены. Держатель опциона при неблагоприятном для него движении цены просто отказывается от своего права, максимальные его убытки не превышают размера премии. Такое асимметричное распределение рисков и необычность структуры сделок делают применение опционов чрезвычайно сложным и требующим точных расчётов и прогнозов. Как подписчик, так и держатель опциона могут закрыть любую открытую позицию до истечения контракта путём заключения офсетной сделки, в результате чего прибыль или убытки определяются разницей в стоимости опциона при открытии и закрытии позиции. 

Существует так называемая справедливая стоимость опциона - теоретически обоснованная минимальная цена, при получении которой подписчик опциона может обеспечить с достаточно большой вероятностью опционные платежи.

Размер рыночной стоимости опциона зависит от следующих факторов:

-        текущего значения базисного актива;

-        отношения между текущим значением базисного актива и ценой исполнения;

-        времени, оставшегося до даты истечения контракта;

-        волатильности цены базисного актива;

-        индивидуальной оценки участников рынка будущей волатильности цены базисного актива;

-        текущих безрисковых процентных ставок (обычно дисконтных ставок краткосрочных казначейских векселей);

-        стиля опциона;

-        текущих значений связанных активов, таких как фьючерсы на базисный актив;

-        специфических особенностей опциона;

-        глубины рынка опциона;

-        влияния спроса и предложения на рынке опционов и на рынке базисного актива;

-        доступной информации о текущих ценах и операциях с рынков базисных активов и рынков связанных активов;

-        индивидуальной оценки участников рынка будущего развития событий в финансовом мире.

В опционах на фьючерсные контракты цены исполнения котируются в пунктах фьючерсной цены. Срок базисных фьючерсных контрактов обычно заканчивается вскоре после даты истечения опционного контракта. Держатель опциона купли на фьючерсный контракт при исполнении опциона открывает длинную позицию по фьючерсному контракту, а также получает сумму денег, равную превышению фьючерсной цены над ценой исполнения, а держатель опциона продажи - короткую и сумму денег, равную превышению цены исполнения над фьючерсной ценой.

Эквивалентным арбитражем называется покупка или продажа комбинаций опционов и наличных позиций, когда между теоретически эквивалентными комбинациями на практике возникает разница цен. Например, комбинация длинной наличной позиции и опциона продажи создаёт опцион купли, а комбинация короткой наличной позиции и опциона купли эквивалентна опциону продажи.

Эквивалентный арбитраж обеспечивает соответствие цен опционов и цен наличного базисного актива, а также поддерживает равновесные цены на опционы купли и продажи. При любом  верна формула паритета цен для опционов купли и продажи европейского стиля на один и тот же базисный актив с одинаковой ценой исполнения (аналогично [6, стр.260]):

,                                                                                                   (3.29)

где S₀ – начальная цена основных активов, С – цена колл-опциона, Р – цена пут-опциона, X – цена исполнения, r – непрерывно начисляемая сложная безрисковая процентная ставка.

При нарушении паритета возникает арбитражная ситуация.

Одним из способов страхования при короткой продаже служит покупка опциона купли. При этом хеджируется только рост стоимости портфеля, но нет защиты от дополнительных требований маржи. Соответственно, прибыль от короткой продажи уменьшается на премию опциона.

Например, прибыли/убытки от полного хеджирования короткой продажи рассчитываются в момент t по формуле:

,                                                                                     (3.30)

,

,

а максимально возможные убытки по формуле:

,                                                                                      (3.31)

где Pr^short – все расходы по поддержанию короткой позиции, за вычетом доходов по ней.

При хеджировании длинной позиции покупкой опциона продажи прибыли/убытки от полного хеджирования рассчитываются по формуле:

,                                                                                      (3.32)

,

, где Pr^long - все расходы по поддержанию длинной позиции, за вычетом доходов по ней.

Модели расчёта премии опциона:

Справедливая стоимость опциона — это обоснованный минимальный платёж покупателя опциона подписчику, получив который подписчик опциона может, используя хеджирующую стратегию, обеспечить гарантированным образом опционные платежи, независимо от случайного состояния цены базисного актива на рынке. Для краткости далее будем справедливую стоимость опциона называть премией, также как и рыночную цену опциона.

Наиболее часто для расчёта цены опциона используется модель Блэка-Шоулса.

Допущения модели:

-        нормальный закон распределения доходности;

-        основные активы свободно продаются и покупаются, в том числе в дробных долях;

-        допускается «короткая» продажа (продажа без покрытия) основных активов, при этом продавец может пускать полученную наличность в оборот;

-        никаких дивидендов или иных выплат по основным активам до исполнения опциона не предусматривается;

-        допускается привлечение и размещение наличности по той же самой безрисковой процентной ставке с непрерывным накоплением процентов;

-        опцион относится к европейскому типу;

-        налоги, расходы на совершение сделок и выплаты маржи отсутствуют;

-        цена основного актива меняется непрерывно с ходом времени, без скачков;

-        характер изменчивости цены основного актива, а также процентная ставка в течение срока опциона остаются постоянными.

Справедливая премия по опциону колл может быть вычислена по следующей формуле [6, стр. 256]:

,                                                                                    (3.33)

где

, .

Связь стоимости колл-опциона со стоимостью пут-опциона была рассмотрена выше.

На практике не все указанные предположения выполняются, и для учёта таких отклонений в основную модель вносят поправки. Но достоинством модели Блэка-Шоулса является простота формул. Поэтому модель адаптирована к различным типам опционов, и часто используется на практике.

Например, в реальном распределении цен вероятности появления значений, сильно отличающихся от среднего значения больше, чем у логарифмически нормального распределения[34]. На практике во многих случаях отказываются от работы со сложными моделями, учитывающими данные несоответствия, а учитывают их наличие, беря при расчёте выгодных и невыгодных опционов увеличенные показатели волатильности. Конкретный пример такого подхода будет приведён в практической части работы.

Для валютного опциона стандартная формула Блэка-Шоулса изменяется с учётом того, что валюта может приносить доход от размещения в депозит. В результате получается так называемая модель Гармана-Кольхагена для валютных опционов [6, стр.258-259]:

,                                                                                (3.34)

где S – текущий обменный курс, r_b – непрерывно начисляемая сложная процентная ставка в валюте, являющейся предметом опциона, r_p – непрерывно начисляемая сложная процентная ставка в валюте, в которой определяется цена опциона,

,         .

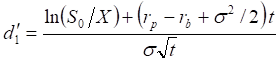Таким образом, для того, чтобы оценить опцион, нужны значения пяти показателей: цена основного актива, процентные ставки, цена и срок исполнения опциона, а также волатильность. Для определения первых двух величин необходимо наличие какой-либо информационной системы, третья и четвертая определяются исходя из решаемой опционом задачи[35], труднее обстоит дело с волатильностью - стандартным отклонением годовой доходности.

Историческая волатильность определяется двумя методами: процентным (если торговля на рынке идёт с перерывами) и логарифмическим (если торговля на рынке непрерывна). Иногда используют усложнённые методы, учитывающие не только значения цены в периоде, но и разницу между максимальными и минимальными ценами в периоде.

Для логарифмического метода:

Доходность можно определить как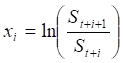, для i=1…n.                         (3.35)

Среднее значение доходности  .                                                           (3.36)

Стандартное отклонение доходности 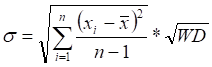,                      (3.37)

 где WD - число рабочих дней в году[36].

При определении волатильности важно выбрать правильную величину рассматриваемого периода, так как цифры, относящиеся к далёкому прошлому, могут быть слабо связаны с текущей волатильностью. Существуют методы определения волатильности, которые учитывают влияние значений доходности на стандартное отклонение с разными весами в зависимости от исторической давности значений.

Для расчётов необходимо применять не историческую, а будущую волатильность и в решении данной задачи кроме значения исторической волатильности важную роль играют: оценка влияния фундаментальных факторов на оцениваемый рынок, оценка ликвидности рынка, проход важных уровней поддержки или сопротивления.

Для измерения риска опционных позиций была создана так называемая греческая таблица. Она объединяет коэффициенты, отражающие влияние изменчивости отдельных факторов на премию опциона. Оценка данных коэффициентов имеет важнейшее значение, в случае если срок опциона отличается от срока хеджируемой сделки.

Коэффициент дельта измеряет влияние волатильности базового актива на цену опциона и определяется как изменение премии при изменении цены основных активов на единицу. Данный коэффициент можно вычислить по следующей формуле (для модели Блэка-Шоулса) на основании [11, стр. 375]:

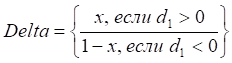,                                                                                   (3.38)

где ,

,  ,

где все указанные переменные соответствуют, приведённым выше при рассмотрении модели Блэка-Шоулса. . Коэффициент дельта равен коэффициенту хеджирования, при хеджировании опциона основными активами. Он показывает, насколько похоже поведение стоимости опциона и цены основных активов. Если дельта близка к нулю, то опцион ведёт себя независимо от основных активов, если коэффициент близок к единице, то стоимость опциона меняется практически синхронно с ценой основного актива.

Коэффициент тета измеряет изменение премии при изменении времени, остающегося до исполнения опциона, на единицу (как правило, - на 1 день).

Тэта может быть рассчитан следующим образом: рассчитываются значения опционных премий в интересующий день и в следующий за ним день, тета равняется разнице между первой и второй премиями.

Коэффициент вега измеряет изменение премии при единичном изменении волатильности (как правило, - на 1%). Рассчитывается как разница между ценой опциона при некотором значении волатильности и ценой опциона при значении волатильности увеличенной на 1%. Значим в основном для долгосрочных опционов.

Коэффициент ро определяется как изменение премии при единичном изменении процентной ставки (как правило, - на 1%). Рассчитывается аналогично тета. Значим в основном для долгосрочных опционов. Коэффициент положителен для колл-опционов и отрицателен для пут-опционов.

Гамма - изменение величины дельта при единичном изменении цены основных активов. Показывает скорость изменения дельта относительно изменения цены базового актива. Может определяться как разница между рассчитанными для цены P₀ и P₁=P₀+1 коэффициентами дельта. Коэффициент гамма всегда больше нуля.

Иногда выделяют также коэффициент, показывающий влияние цены рынка на коэффициент гамма. Он носит название gamma of the gamma.

Лямбда - выраженное в процентах изменение премии при единичном изменении цены основных активов. Рассчитывается как отношение коэффициента дельта к частному от деления премии за опцион на цену основных активов.

При оценке портфеля рассчитывают суммарные позиции по каждому из коэффициентов. Использующиеся при расчёте наиболее значимых позиций правила, я для удобства свёл в одну таблицу 3:

 

Таблица 3. Значения возникающих позиций при проведении операций

	Коэффициенты
Операция	Delta	Gamma	Vega	Theta
Покупка фьючерса	+1	0	0	0
Продажа фьючерса	-1	0	0	0
Покупка колл-опциона	+delta	+gamma	+vega	+theta
Продажа пут-опциона	+delta	- gamma (в delta +)	-vega	-theta
Покупка пут-опциона	-delta	+gamma (в delta +)	+vega	+theta
Продажа колл-опциона	-delta	-gamma	-vega	-theta

3.3. Управление риском акций

В настоящем разделе будет рассмотрен вопрос выбора стратегии защиты стоимости портфеля акций, находящихся в собственности банка. В данном случае целью банка является следующая: установить нижнюю границу стоимости портфеля, ниже которой она опуститься не может, но оставить возможность использовать повышение курса акций.

Все такие стратегии включают в себя покупку опционов для обеспечения нужной степени защиты.

Наиболее распространены следующие три схемы:

- покупка пут-опционов;

- ликвидация портфеля акций и покупка колл-опционов;

- покупка коллара.

Первый вариант является самым простым способом. Покупка справедливых или выгодных пут-опционов устанавливает нижнюю границу цены, по которой можно будет реализовать акции из портфеля, при этом у банка будет неограниченная прибыль при повышении стоимости портфеля. Главным недостатком схемы является существенные затраты на премию.

Данный вариант по экономическим последствиям от изменения цены активов мало чем отличается от первого.

Основой третьего варианта является продажа «невыгодных» колл-опционов и покупка на вырученные средства пут-опционов. Таким образом, банк ограничивает возможную прибыль от роста стоимости пакета акций, но снижает стоимость хеджирования. Схема эффективна тогда, когда банк не ожидает большого роста стоимости акций входящих в портфель в хеджируемый период.

Принимая решение о хеджировании позиции с помощью той или иной опционной стратегии, в случае альтернативных вариантов банк должен подсчитать затраты, связанные с каждой стратегией и выбрать наиболее дешёвую из них. При определении стоимости хеджирования следует учитывать комиссионные за покупку-продажу опциона и актива, а также возможность разместить полученные средства при подписке опциона под безрисковый процент на требуемый срок, неполученный безрисковый процент на сумму премии при покупке опциона и неполученные дивиденды при продаже акций.

Если необходимо хеджировать стоимость портфеля от риска падения рынка, но при этом оставить возможность участия в прибыли при движении рынка вверх, можно открыть длинную позицию в опционе продажи "при деньгах" на индексный фьючерсный контракт. Если по окончании хеджа фьючерсная цена не изменится или возрастёт, то опцион истекает ничего не стоящим и полная премия является расходом на страхование. Если же фьючерсная цена упадёт на несколько пунктов, то опцион истекает "в деньгах" и рост опционной премии покрывает часть убытков в стоимости портфеля.